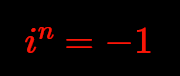
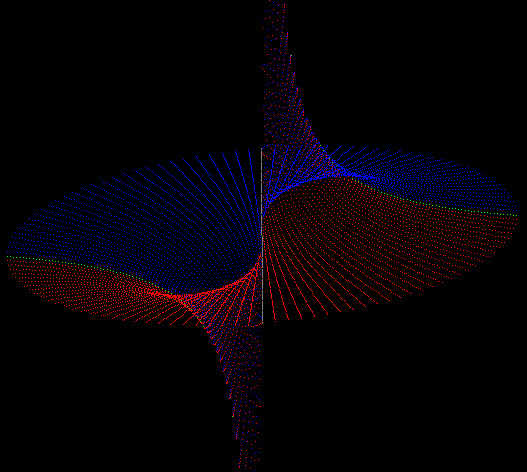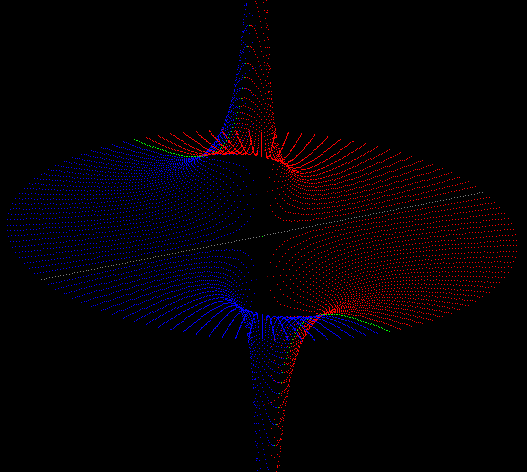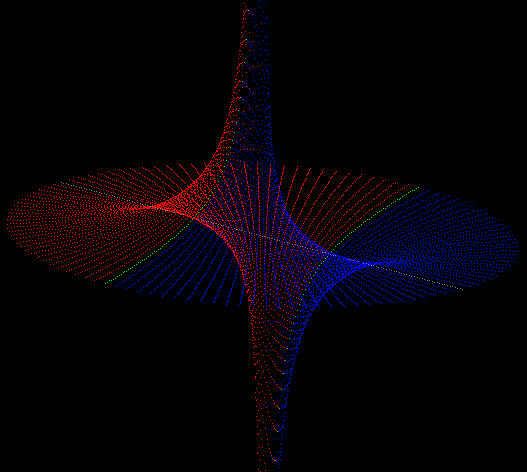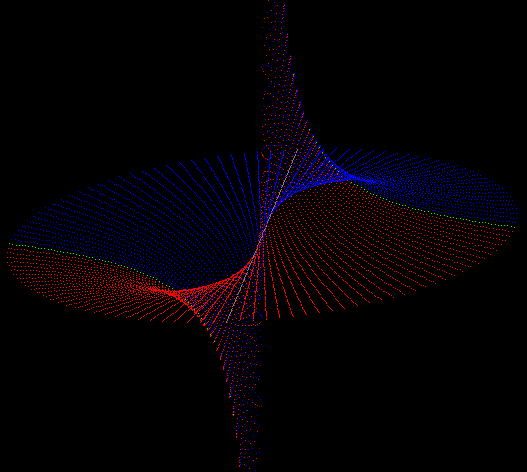
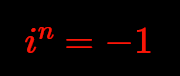
A vector $\vec x \in \mathbb R^n$ is zero divisor, if the determinant of its multiplication matrix is zero.

Determinants have the habit specially with growing dimension to become more and more complicated. And this makes general statements sometimes very difficult. In our case, we can factorize the determinant of the multiplication matrix for every $n>2$:

$det \left( M_{\Large{n={\color{blue}{1+}}2k}} \right) = \color{blue}{\sum\limits_{i=0}^{n-1} \left( {(-1)^{n} \over n} x_i \right) \cdot}$ $\prod\limits_{l=0}^{k-1} \sum\limits_{i=0}^{n-1} \sum\limits_{j=0}^{n-1} cos \left( {(2l+1)(i-j) \over n} π \right) x_i x_j$

The difference between the determinants in odd- and even-dimensional vector spaces is in blue color. To recognize what these factors are, is in this representation very difficult. At least for the blue factor there is the expression of a hyperplane, an (n-1)-dimensional vector subspace defined in geometry, but I found this word always little confusing and there is no special definition for (n-2)-dimensional vector subspaces (luckily). These are most of the factors, written as double sums.

Their geometrical strucutre of the factors is much easier to recognize with the assistance of the scalar product ($\circ$):

$det \left( M_{\Large{n={\color{blue}{1+}}2k}} \right) = \color{blue}{ \left( \vec x \circ {\hat r_k \over | \hat r_k |^2 } \right) \cdot }$ $\prod\limits_{j=0}^{k-1} \left( \left( \vec x \circ {\hat r_j \over | \hat r_j |^2 }\right)^2 + \left( \vec x \circ {\hat i_j \over | \hat i_j |^2 }\right)^2\right)$

A scalar product is zero, if its factors are perpendicular. This means, the blue factor (for odd n) is zero if $\vec x$ is perpendicular to the vector $\hat r_k$. And there are k factors, of which is one zero, if $\vec x$ is perpendical to two vectors, $\hat r_j$ and $\hat i_j$, with valid indices for j: $j \in \{0,1,\ldots,k-1\}$.

The hat on these vectors should point out, that they are some kind of unit vectors. I call them atomic unit vectors or the unit vectors of the atomic vector subspaces.